Projective cover

In the branch of abstract mathematics called category theory, a projective cover of an object X is in a sense the best approximation of X by a projective object P. Projective covers are the dual of injective envelopes.

1 Definition
2 Properties
3 Examples
4 See also
5 References

Definition

Let 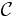$\mathcal{C}$ be a category and X an object in 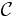$\mathcal{C}$ . A projective cover is a pair (P,p), with P a projective object in 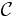$\mathcal{C}$ and p a superfluous epimorphism in Hom(P, X).

If R is a ring, then in the category of R-modules, a superfluous epimorphism is then an epimorphism 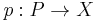$p�: P \to X$ such that the kernel of p is a superfluous submodule of P.

Properties

Projective covers and their superfluous epimorphisms, when they exist, are unique up to isomorphism.

The main effect of p having a superfluous kernel is the following: if N is any proper submodule of P, then 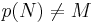$p(N) \ne M$ ^[1]. Informally speaking, the superfluous kernel causes P to cover M optimally, in some sense. This does not depend upon the projectivity of P, it is true of all superfluous epimorphisms.

If (P,p) is a projective cover of M, and P' is another projective module with an epimorphism 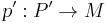$p':P'\rightarrow M$ , then there is a split epimorphism α from P' to P such that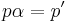 $p\alpha=p'$

Unlike injective envelopes, which exist for every left (right) R-module regardless of the ring R, left (right) R-modules do not in general have projective covers. A ring R is called left (right) perfect if every left (right) R-module has a projective cover in R-Mod (Mod-R).

A ring is called semiperfect if every finitely generated left (right) R-module has a projective cover in R-Mod (Mod-R). "Semiperfect" is a left-right symmetric property.

A ring is called lift/rad if idempotents lift from R/J to R, where J is the Jacobson radical of R. The property of being lift/rad can be characterized in terms of projective covers: R is lift/rad if and only if direct summands of the R module R/J (as a right or left module) have projective covers. (Anderson, Fuller 1992, p. 302)

Examples

In the category of R modules:

If M is already a projective module, then the identity map from M to M is a superfluous epimorphism (its kernel being zero). Hence, projective modules always have projective covers.
If J(R)=0, then a module M has a projective cover if and only if M is already projective.
In the case that a module M is simple, then it is necessarily the top of its projective cover, if it exists.
The injective envelope for a module always exists, however over certain rings modules may not have projective covers. The class of rings which provides all of its right modules with projective covers is the class of right perfect rings.

References

^ Proof: Let N be proper in P and suppose p(N)=M. Since ker(p) is superfluous, ker(p)+N≠P. Chose x in P outside of ker(p)+N. By the surjectivity of p, there exists x' in N such that p(x' )=p(x ),, whence x−x' is in ker(p). But then x is in ker(p)+N, a contradiction.

Anderson, Frank Wylie; Fuller, Kent R (1992). Rings and Categories of Modules. Springer. ISBN 0387978453. http://books.google.com/books?id=PswhrD_wUIkC. Retrieved 2007-03-27.

Faith, Carl (1976), Algebra. II. Ring theory., Grundlehren der Mathematischen Wissenschaften, No. 191. Springer-Verlag

Lam, T. Y. (2001), A first course in noncommutative rings. (2nd ed.), Graduate Texts in Mathematics, 131. Springer-Verlag, ISBN 0-387-95183-0

Projective cover

Contents

Definition

Properties

Examples

See also

References